The Simplex Method in Matrix Form: A Step-by-Step Guide

The Simplex Method is one of the most powerful techniques for solving linear programming (LP) problems. It efficiently finds the optimal solution by iterating through corner points of the feasible region. The matrix form of the Simplex Method provides a structured approach to solving LP problems using tableau representation. In this post, we’ll break down the matrix formulation of the Simplex Method and walk through its key steps.

1. Formulating the Linear Program in Standard Form

Before applying the Simplex Method, we must express our linear program in standard form:

Mathematical formula on a black background reads: Maximize Z = c₁x₁ + c₂x₂ + ... + cₙxₙ. White text, clear and focused.

Subject to:

Mathematical inequalities in white on a black background, featuring variables and coefficients. Emphasizes linear equations and non-negative constraints.

Step 1: Convert Inequalities into Equations

We introduce slack variables:

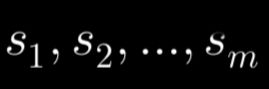
Text on a black background showing symbols: s₁, s₂, ..., sₘ. The font is white and serif, suggesting a mathematical or formal context.

to transform the inequalities into equalities:

Mathematical inequalities on a black background. Equations involve variables x1 to xn with coefficients and constraints, plus x ≥ 0.

Now, the objective function is:

Mathematical equation in white font on a black background: Z = c₁x₁ + c₂x₂ + ... + cₙxₙ + 0s₁ + 0s₂ + ... + 0sₘ.

2. Constructing the Simplex Tableau (Matrix Form)

The linear program is now represented in tabular form, which consists of the following components:

1. Coefficients of decision variables and slack variables

2. Right-hand side (RHS) values

3. Objective function row

The initial Simplex tableau is structured as follows:

Simplex method tableau showing Basis, variables \(x_1\) to \(x_n\), slack variables \(s_1\) to \(s_m\), and RHS values \(b_1\) to \(b_m\). Black background.

Where:

• The basis column tracks which variables are currently in the solution.

• The RHS column represents the values of the basic variables.

• The Z-row represents the coefficients of the objective function.

3. Iterative Steps of the Simplex Algorithm

The algorithm follows these key steps:

Step 1: Identify the Pivot Column (Entering Variable)

• Find the most negative value in the Z-row (excluding the RHS).

• The corresponding column is the pivot column, indicating which variable will enter the basis.

Step 2: Identify the Pivot Row (Leaving Variable)

• Compute the minimum ratio test:

Text with white font on black background says "RHS Pivot Column Coefficients" with a horizontal line between words.

• The smallest non-negative ratio determines the pivot row, indicating which variable will leave the basis.

Step 3: Perform Row Operations (Pivoting)

• Normalize the pivot row so that the pivot element becomes 1.

• Eliminate other entries in the pivot column using row operations.

Step 4: Repeat Until Optimality

• Continue iterating until all values in the Z-row (except RHS) are non-negative, indicating that the optimal solution has been reached.

4. Example of the Simplex Method in Matrix Form

Consider the following LP problem:

White text on black background shows a mathematical expression: "Maximize Z = 3x1 + 5x2".

Subject to:

Mathematical inequalities on a black background: x₁ + 2x₂ ≤ 4, 3x₁ + 2x₂ ≤ 6, and x₁, x₂ ≥ 0.

Step 1: Convert to Standard Form

Introduce slack variables s1 and s2:

Two mathematical equations, \(x_1 + 2x_2 + s_1 = 4\) and \(3x_1 + 2x_2 + s_2 = 6\), in white on a black background.

Step 2: Initial Simplex Tableau

Simplex table on black background showing basis, variables \(x_1, x_2\), slack variables \(s_1, s_2\), and RHS values.

• The most negative value in the Z-row is -5 → Pivot column: x2.

• Compute the minimum ratio test:

Equations "4/2=2" and "6/2=3" in white text on a black background, each preceded by a white dot, creating a simple, focused math display.

→ Pivot row: s1, Pivot element: 2

Step 3: Perform Pivoting & Iterate

• Normalize row operations.

• Repeat steps until all Z-row values are non-negative.

• Extract the optimal solution when the process terminates.

5. Conclusion

The Simplex Method in matrix form provides a structured way to solve linear programs efficiently. By setting up the problem as a tableau, identifying the pivot elements, and iterating through row operations, we systematically reach the optimal solution. This method is widely used in operations research, economics, and engineering to solve real-world optimization problems.

Want to learn more? Watch our detailed video series on the Simplex Method on our YouTube channel!

The Simplex Method in Matrix Form: A Step-by-Step Guide